交叉验证相关理论介绍
2020.10.13
1.1 场景构建
源禾同学和正阳同学在某次考试都考了100分,正阳同学实力强劲,学习踏实,掌握核心科技,考了100是实力的体现,因为卷子上只有100分。而源禾同学考100分,因为源禾使用了败者食尘,他课下做了这张卷子的所有题,背了题,考了100分是因为记性好。
谁才是老师喜爱的同学呢?
在对模型进行测试时,不可以照着“考卷”疯狂练习。尤其是在样本量小的时候,换一张卷子就会原形毕露。
那么不妨站在老师的角度想,如果题库只有这么多题,该怎么出题才能真正考察学生的实力呢?
1.2 模型/算法的选择
在建模时,可选用的模型很多,我们想选用何种模型,此时就需要对模型的“泛化误差”(generalization-error,指在独立测试样本上的期望预测误差,也称测试误差test-error或预测误差prediction-error)进行评估。
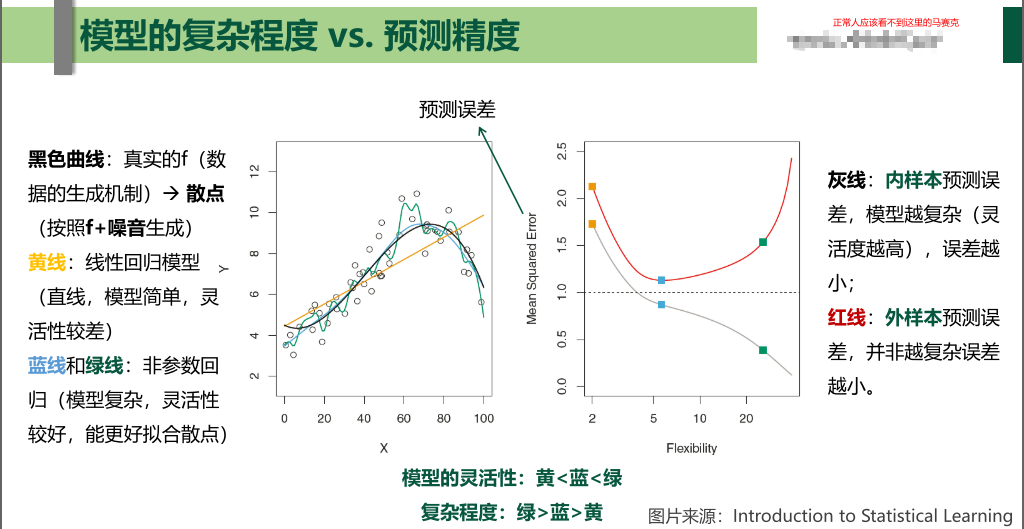
在实际建模中,很少能得到样本的精确分布,也无法直接计算泛化误差。基于训练样本得到的样本上平均损失的训练误差是它的一个直接估计,可训练误差会随着模型复杂度(光滑度,自由度)的增加而减小,直至减小到0。(训练均方误差 vs 测试均方误差)
如果训练均方误差很小但测试均方误差较大时,我们称该数据被过拟合。(模型开始背题了)
源禾:任何难处都可以靠增加数据量来解决。
(当然解决不了的除外)
事实上,这里涉及到偏差方差权衡(bias-variance trade-off)的问题,如果一个统计模型被称为测试性能好,那么要去该模型具有较小的方差和较小的偏差。直觉上我们会选择有极小偏差可是有很大方差的方法(如画一条通过所有观测的曲线,下图的绿线)
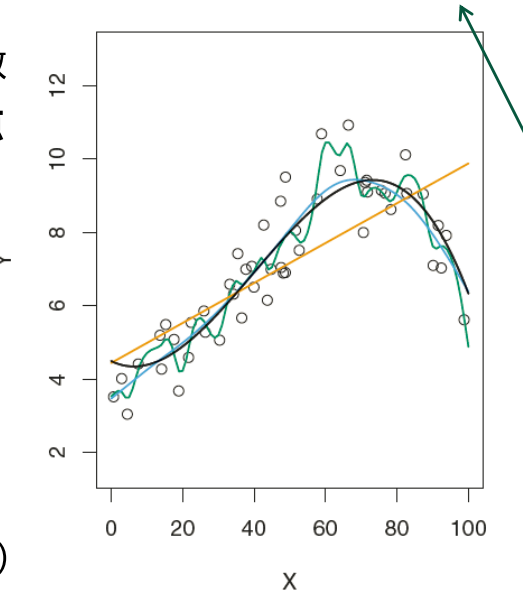
源禾:虽然没有完美的模型,但是有完美模型的传说。
为一个模型来选择何适的光滑度的过程即模型选择。这个问题在训练集较小时,被产生的过拟合现象加大了难度。
1.3 出路 - 重抽样(resampling)
应当找到一个方法解决过拟合,而唯一的限制是,没那么多数据。
于是人们想了个办法:让这个测试集来源于训练集。我反复从训练集中抽取样本,对每一个样本重新拟合一个模型,来获取关于拟合模型的附加信息。这就是重抽样方法。在拟合过程中,保留(holding out)训练观测的一个子集,然后对保留的观测运用统计学习方法,从而来估计其测试错误率(test error rate)。
源禾:预测集神圣不可侵犯。
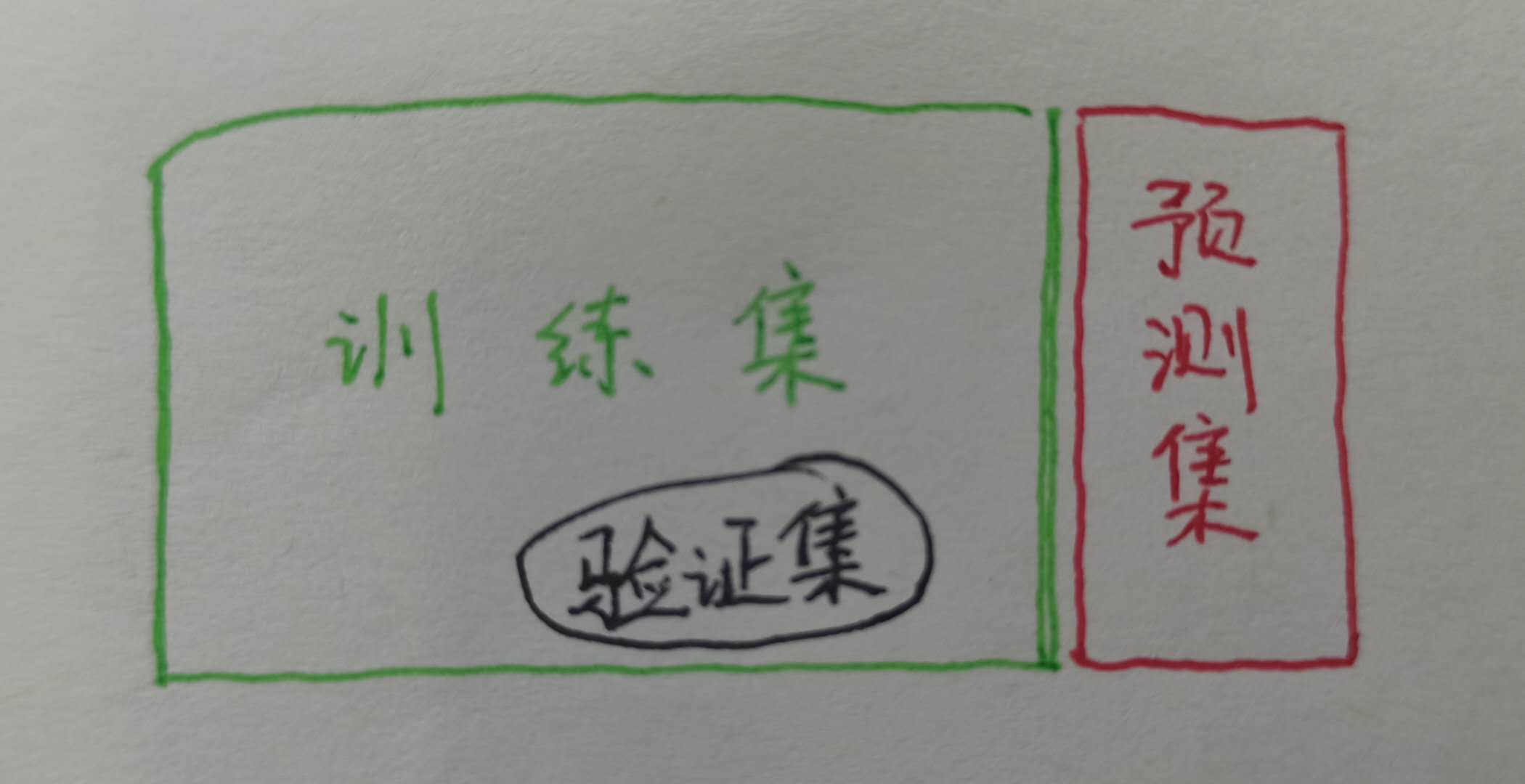
2.1 验证集方法(validation set approach)
首先随机地把观测集分成两部分:一个训练集(training set),一个验证集(validation set),或者叫保留集(hold-out set)。模型在训练集上拟合,然后用拟合的模型来预测验证集中观测的响应变量。最后得到的验证集错误率——通常用均方误差作为定量响应变量的误差度量——提供了对于测试错误率的一个估计。
附一个“上帝”的比例:70%的训练集,30%的测试集。
验证集方法原理简单,易于执行,但它有两个潜在的缺陷:
1.测试错误率的验证法估计的波动很大,这取决于具体哪些观测被包括在训练集中,哪些观测被包括在验证集中。
2.在验证法中,只有一部分观测被用于拟合模型,由于被训练的观测越少,统计方法的表现越不好,意味着验证集错误率可能会高估在整个数据集上拟合模型的测试错误率。
统计分析中通过多次重复试验来减小方差。
2.2 留一交叉验证(leave-one-out cross-validation)
留一交叉验证(LOOCV)与验证集方法很相似,但这种方法尝试解决验证集方法遗留的缺陷问题。
LOOCV将观测集分为两部分,但不同于把观测集分为两个大小相当的子集,留一交叉验证法将一个单独的观测$(x_1, y_1)$作为验证集,剩下的观测$\{(x_2, y_2),(x_3, y_3), … ,(x_n, y_n)\}$组成训练集。由于拟合中没有用到$(x_1, y_1)$,所以$MSE_1 = (y_1 - \hat{y_1})^2$ 提供了对于测试误差的一个渐进无偏估计。
能看出,由于$MSE_1$是基于一个单独的观测计算得出的,故具有很高的波动性。
重复上面计算$MSE_1$的步骤,计算出全部的$MSE_1, MSE_2, …, MSE_n$,对测试均方误差的LOOCV估计是这n个测试误差估计的均值:
相对于验证集方法,LOOCV方法更不容易高估测试错误率,也能彻底解决训练集和验证集分割时随机性导致的结果不同问题。
2.3 K折交叉验证(K-fold CV)
k折交叉验证法是LOOCV的一个替代,这种方法将观测集随机地分成K个大小基本一致的组,或者说折(fold)。第一折作为验证集,然后在剩下的k-1折上拟合模型。均方误差$MSE_1$由保留的观测计算得出。
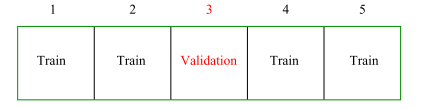
重复这个步骤k次(注意一般k大于2),每一次把不同的观测组作为验证集(分组只是第一次分)。整个过程会得到k个测试误差的估计,$MSE_1, MSE_2, …, MSE_k$。k折CV估计由这些值求平均计算得到:
不难发现,k等于n时,LOOCV方法是k折交叉验证的一个特例。
k一般取5或10。不取n的原因果然还是因为好算啊。几乎对于任一种统计学习方法适用,都有更好的可行性。
源禾:在计算简便和尽可能减少估计的波动面前,一个能“我全都要”的方法谁不喜欢呢?
k折交叉验证的结果也会因观测分折的随机性产生一定波动。同时对$Err$估计时也会因训练集样本容量大小产生一定的高估。
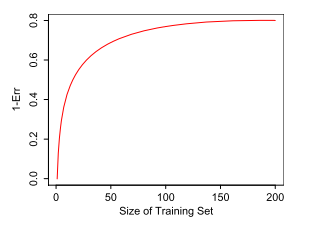
由上图可知,训练集在150+时,训练效果已经不再随着训练集样本量增加而增加。但训练集样本容量在0至50时,会明显低估$1-Err$。
2.4 总结
先画一张表在这:
| 方法 | 优点 | 缺点 | 计算复杂度 |
|---|---|---|---|
| 验证集方法(validation set approach) | 原理简单,易于执行 | A.测试错误率的验证法估计的波动很大,与分组关系很大。B.验证集错误率可能会高估在整个数据集上拟合模型的测试错误率。 | 计算最简单,方便对比称一个计算单步(对数据进行多次重复划分时计算复杂度会相应高) |
| 留一交叉验证法(Leave-one-out cross-validation) | A.偏差较小,不易高估错误率。训练模型最接近原始样本的分布。B.LOOCV方法能解决训练集和验证集分割的随机性。实验可复制。 | A.模型需拟合n次,非常耗时。(但是最小二乘法来拟合线性或多项式回归时只消耗一个计算单步)B.方差较大。 | 除左栏提到的线性/多项式回归外,需要n个计算单步。大样本情况时,对于某些算法来说数据划分为n份也不可接受。svm和朴素贝叶斯分类器。 |
| k折交叉验证(k-fold CV) | A.偏差问题不大,方差较小。有效避免过拟合和欠拟合情况发生。B.计算方便,计算开销小。 | A.选择K折交叉验证的“K”时比较随机。B.会产生一定波动。偏差大小会随训练集样本容量变化而改变。 | k个计算单步 |
k折CV方法相对于LOOCV方法除了计算优势外,它对测试错误率的估计通常来说更加准确。
| 验证集方法 | LOOCV方法 | k折CV方法 | |
|---|---|---|---|
| 偏差角度 | 高估 | 近似无偏 | 中等程度偏差 |
| 方差角度 | k<n时方差大于k折CV方法 | k<n时方差小于LOOCV方法 |
由上表可知,选择方法时,需要进行偏差-方差权衡。在选择k折CV的折数时,一般k=5或10使得测试错误率的估计不会有过大的偏差或方差。
2.5 补充
一、
之前提到交叉验证方法可以应用于多个场景,举个例子,交叉验证在分类器模型的应用:
其实只需要修改“泛化误差”为“损失函数”($MSE$ to $Err$),比如k折CV错误率的形式:
其中$Err_i = I(y_i \ne \hat{y_i}) $。LOOCV和验证集错误率也可类似定义。
二、
上文提到,在LOOCV方法中,最小二乘法来拟合线性或多项式回归时将只计算一次。
其中$\hat{y_i}$为用原始最小二乘拟合的第i个拟合值,$h_i$为杠杆统计量:
区别仅在于第i个残差除了一个系数$(1-h_i)$。杠杆值的大小在0到1之间,反映了一个观测对自己拟合值的影响大小。因此,该公式表明高杠杆值的残差根据它本身偏离数据的程度进行了等量的放大。
三、
若样本量非常小,非常非常小,我们还可以使用重抽样的另一种方法:自助法(bootstrap)。
比如我们有m个样本(m较小),每次在这m个样本中随机采集一个样本,放入训练集,采样完后把样本放回。这样重复采集m次,我们得到m个样本组成的训练集。当然,这m个样本中很有可能有重复的样本数据。同时,用原始的m个样本做测试集。这样接着进行交叉验证。
参考文献
[1]James G , Witten D , Hastie T , et al. An Introduction to Statistical Learning[M]. Springer New York, 2013.
[2]杨柳,王钰.泛化误差的各种交叉验证估计方法综述[J].计算机应用研究,2015,32(05):1287-1290+1297.
[3]范永东. 模型选择中的交叉验证方法综述[D].山西大学,2013.
[4]Hastie, Trevor J. The Elements of Statistical Learning[M]. 世界图书出版公司, 2015.
本文链接: https://konelane.github.io/2020/10/13/201010CV/
-- EOF --
转载请注明出处 署名-非商业性使用-禁止演绎 3.0 国际(CC BY-NC-ND 3.0)


