目录

最后编辑于：2020.02.05 12:30

Numpy库

Numpy库是Python的一种开源的数值计算扩展。

Numpy可用来存储和处理大型矩阵，比Python自身的嵌套列表结构要高效很多。

据说Numpy将Pyhon变成了一种免费的更强大的Matlab系统。

本文介绍性文字转载自万旷网。氦核感觉notebook形式更适合学习，有机会把丘比特文件给大家附上。

Numpy库包含了：

>

强大的N维数组对象
精密的函数
连接C/C++和Fortran代码的工具
常用的线性代数，傅里叶变换和随机数生成

1
2

#首先导入 numpy 库
import numpy as np

氦核：惯用的导入法，最好延用。

一、数组array

数组array和列表list类似，但是数据array可以定义维度，且适合做数学代数运算

1.数组array生成

数据使用windapi提取。

1
2
3
4
5

from WindPy import *
w.start()
a = w.wsd("000001.SZ", "close", "2018-07-05", "2018-07-11", "")
b = w.wsd("000002.SZ", "close,open", "2018-07-05", "2018-07-11", "")
b

氦核：取的是收盘价和开盘价。

.ErrorCode=0
.Codes=[000002.SZ]
.Fields=[CLOSE,OPEN]
.Times=[20180705,20180706,20180709,20180710,20180711]
.Data=[[23.05,23.21,24.01,24.15,23.46],[23.02,23.34,23.37,24.2,23.48]]

1
2
3
4
5
6
7
8
9

a1 = np.array(a.Data[0])
a2 = np.array(b.Data)
print('这是一个一维数组：\n',a1)
print()
print('这是一个二维数组：\n',a2)
print()
print('查看a1的长度：\n',len(a1))
print()
print('查看a2的长度：\n',len(a2))

氦核：len可以求数组长度，指数组里有几个list。

这是一个一维数组：
 [8.6  8.66 9.03 8.98 8.78]

这是一个二维数组：
 [[23.05 23.21 24.01 24.15 23.46]
 [23.02 23.34 23.37 24.2  23.48]]

查看a1的长度：
 5

查看a2的长度：
 2

1

a2

array([[23.05, 23.21, 24.01, 24.15, 23.46],
       [23.02, 23.34, 23.37, 24.2 , 23.48]])

1

a2[0,1]

23.21

1.2 数组array性质

1
2
3
4

'''数组元素整数转化为浮点数'''
print('数组类型：',a1.dtype)
float_arr = a1.astype(np.int)
print('改变数组类型后：',float_arr.dtype)

氦核：dtype可以查看类型，astype可以转换类型。不同类型变换后会产生不同结果。

数组类型： float64
改变数组类型后： int32

1
2
3
4

'''字符串数字转化为浮点数'''
numeric_string = np.array(['1.11','2.22','3.33'])
print(numeric_string, numeric_string.dtype)
print(numeric_string.astype(np.float),numeric_string.astype(np.float).dtype)

['1.11' '2.22' '3.33'] <U4
[1.11 2.22 3.33] float64

1
2
3
4

'''字符串数字转化为浮点数'''
numeric_string = np.array(['1.11','2.22','3.33'])
print(numeric_string, numeric_string.dtype)
print(numeric_string.astype(np.float),numeric_string.astype(np.float).dtype)

['1.11' '2.22' '3.33'] <U4
[1.11 2.22 3.33] float64

1
2
3
4
5
6
7
8
9
10
11

print(a2)
print()
print('第二行第三列元素(第二行索引为1，第三列索引为2)：\n',a2[1,2]) 
print()
print('倒数第一行(注意索引为-1)：\n',a2[-1,:]) 
print()
print('第三列(索引为2)：\n',a2[:,2])
print()
print('a2形状：\n',a2.shape)
print()
print('a2形状重构：\n',a2.reshape(5,2))

[[23.05 23.21 24.01 24.15 23.46]
 [23.02 23.34 23.37 24.2  23.48]]

第二行第三列元素(第二行索引为1，第三列索引为2)：
 23.37

倒数第一行(注意索引为-1)：
 [23.02 23.34 23.37 24.2  23.48]

第三列(索引为2)：
 [24.01 23.37]

a2形状：
 (2, 5)

a2形状重构：
 [[23.05 23.21]
 [24.01 24.15]
 [23.46 23.02]
 [23.34 23.37]
 [24.2  23.48]]

1
2
3
4
5
6
7
8
9
10
11
12
13

print('维度解锁：',a2.ravel())  #  ravel()函数可以将高维数组转化为一维数组
print()
print('按列求和：',a2.sum(axis=0))
print()
print('按列求积：',a2.prod(axis=0))
print()
print('全局最大值：',a2.max(),'全局最小值：',a2.min())
print()
print('按行求最大值：',a2.max(axis=0),'按列求最小值：',a2.min(axis=1))
print()
print('按列求均值：',a2.mean(axis=0))
print()
print('按行求标准差：',a2.std(axis=0))

维度解锁： [23.05 23.21 24.01 24.15 23.46 23.02 23.34 23.37 24.2  23.48]

按列求和： [46.07 46.55 47.38 48.35 46.94]

按列求积： [530.611  541.7214 561.1137 584.43   550.8408]

全局最大值： 24.2 全局最小值： 23.02

按行求最大值： [23.05 23.34 24.01 24.2  23.48] 按列求最小值： [23.05 23.02]

按列求均值： [23.035 23.275 23.69  24.175 23.47 ]

按行求标准差： [0.015 0.065 0.32  0.025 0.01 ]

氦核：这些计算都是可以接受方向的。按列或按行。

1
2
3
4
5
6
7

print('原矩阵：\n',a2)
print()
print('按列求和：\n',a2.sum(axis=0))
print()
print('按行求均值：\n',a2.mean(axis=1))
print()
print('按行累加：\n',a2.cumsum(axis=1))

原矩阵：
 [[23.05 23.21 24.01 24.15 23.46]
 [23.02 23.34 23.37 24.2  23.48]]

按列求和：
 [46.07 46.55 47.38 48.35 46.94]

按行求均值：
 [23.576 23.482]

按行累加：
 [[ 23.05  46.26  70.27  94.42 117.88]
 [ 23.02  46.36  69.73  93.93 117.41]]

1
2
3

print('矩阵所有元素求指数：\n',np.exp(a2))
print()
print('矩阵所有元素求根号：\n',np.sqrt(a2))

氦核：np.exp功能是“求e的幂次方”。

矩阵所有元素求指数：
 [[1.02444302e+10 1.20219502e+10 2.67553422e+10 3.07759692e+10
  1.54364896e+10]
 [9.94166153e+09 1.36909381e+10 1.41078893e+10 3.23538868e+10
  1.57483274e+10]]

矩阵所有元素求根号：
 [[4.80104155 4.81767579 4.9        4.91426495 4.84355242]
 [4.79791621 4.83114893 4.83425279 4.91934955 4.84561658]]

小数位数控制和取整

1

print('小数位数：\n',a1.round(decimals=2)) #控制小数位数

小数位数：
 [8.6  8.66 9.03 8.98 8.78]

1
2
3
4
5
6
7

print('原数组：\n',a1)
print()
print('向上取整：\n',np.floor(a1))
print()
print('向下取整：\n',np.ceil(a1))
print()
print('四舍五入(控制小数为2位)：\n',np.round(a1,2))

原数组：
 [8.6  8.66 9.03 8.98 8.78]

向上取整：
 [8. 8. 9. 8. 8.]

向下取整：
 [ 9.  9. 10.  9.  9.]

四舍五入(控制小数为2位)：
 [8.6  8.66 9.03 8.98 8.78]

数组——一元函数

1.3 数组array间运算

1
2
3

c, r = np.array([1,2,3,4]), np.array([2,3,4,5])
print(c)
print(r)

[1 2 3 4]
[2 3 4 5]

1
2
3
4
5

print('数组相加：',c + r)
print('数组相乘：',c * r)
print('数组乘方：',c **r)
print('数组判断：',c >= 2)
print('向量内积：',c.dot(r.T))

数组相加： [3 5 7 9]
数组相乘： [ 2  6 12 20]
数组乘方： [   1    8   81 1024]
数组判断： [False  True  True  True]
向量内积： 40

1
2

print('取两个数组中的较大值组成新的数组：',np.maximum(c,r))
print('取两个数组中的较小者组成新的数组：',np.minimum(c,r))

取两个数组中的较大值组成新的数组： [2 3 4 5]
取两个数组中的较小者组成新的数组： [1 2 3 4]

1
2
3
4
5
6
7

x1 = np.array([True,False,True])
x2 = np.array([False,False,True])
print(x1)
print(x2)
print(np.logical_and(x1,x2))
print(np.logical_or(x1,x2))
print(np.logical_xor(x1,x2))

氦核：逻辑运算一样很简单，logical_xor是异或运算。一般逻辑函数用于检验数组内容，筛选出需要的元素（通常得到的是位置）。可以完成“检查a中元素是否存在于b中”这样的问题。简便操作详细见下面集合运算。

[ True False  True]
[False False  True]
[False False  True]
[ True False  True]
[ True False False]

数组——二元函数

1.4 数组array集合运算

1
2
3
4
5
6
7
8
9
10
11
12
13

x = np.array([1,2,3,3,3,3,4,5,10,10,20,30])
y = np.array([100,20,40,10,3,2,1])
print('数组x中的唯一元素：\n',np.unique(x))
print()
print('数组x和y的公共元素：\n',np.intersect1d(x,y))
print()
print('数组x和y的并集：\n',np.union1d(x,y))
print()
print('数组x中的元素是否包含于y：\n',np.in1d(x,y))
print()
print('集合差_在x中而不在y中的元素：\n',np.setdiff1d(x,y))
print()
print('只存在某个数组中，而不同时存在于两个数组中：\n',np.setxor1d(x,y))

数组x中的唯一元素：
 [ 1  2  3  4  5 10 20 30]

数组x和y的公共元素：
 [ 1  2  3 10 20]

数组x和y的并集：
 [  1   2   3   4   5  10  20  30  40 100]

数组x中的元素是否包含于y：
 [ True  True  True  True  True  True False False  True  True  True False]

集合差_在x中而不在y中的元素：
 [ 4  5 30]

只存在某个数组中，而不同时存在于两个数组中：
 [  4   5  30  40 100]

1.5 数组array切片进阶

1
2

#还是以000001收盘价为例
a1

array([8.6 , 8.66, 9.03, 8.98, 8.78])

1
2
3
4
5

# 如果我们想 按偶数来选取 即选择数组中的0,2,4,6,8
print(a1[::2])

# 如果想 按奇数来选择呢
print(a1[1::2]) #这里的1表示从索引1开始截取

氦核：上面片段中的2代表步长。

[8.6  9.03 8.78]
[8.66 8.98]

1
2
3
4
5
6
7

#我们取多个指标看一下

#五粮液
from WindPy import *
w.start()
w = w.wsd("000858.SZ", "open,high,low,close,pct_chg", "2018-07-05", "2018-07-11", "")
w

氦核：开，高，低，收。

.ErrorCode=0
.Codes=[000858.SZ]
.Fields=[OPEN,HIGH,LOW,CLOSE,PCT_CHG]
.Times=[20180705,20180706,20180709,20180710,20180711]
.Data=[[71.69,69.9,71.58,73.57,71.2],[72.71,71.98,73.55,74.13,72.64],[69.7,68.88,70.4,72.08,70.93],[70.82,70.62,73.54,73.37,72.08],[0.16973125884014886,1.5822798147378172,4.134806003964902,-0.23116671199347652,-1.7582118031893383]]

1
2

w1 = np.array(w.Data)
w1

array([[71.69      , 69.9       , 71.58      , 73.57      , 71.2       ],
       [72.71      , 71.98      , 73.55      , 74.13      , 72.64      ],
       [69.7       , 68.88      , 70.4       , 72.08      , 70.93      ],
       [70.82      , 70.62      , 73.54      , 73.37      , 72.08      ],
       [ 0.16973126,  1.58227981,  4.134806  , -0.23116671, -1.7582118 ]])

1
2
3
4
5

print('截取第1行第4,5个元素：\n',w1[0, 3:5])
print()
print('截取第5行至最后，第5列至最后的元素：\n',w1[4:, 4:])
print()
print('截取第3，5行，第1,3,5列\n',w1[2::2, ::2])

截取第1行第4,5个元素：
 [73.57 71.2 ]

截取第5行至最后，第5列至最后的元素：
 [[-1.7582118]]

截取第3，5行，第1,3,5列
 [[69.7        70.4        70.93      ]
 [ 0.16973126  4.134806   -1.7582118 ]]

1.6 数组排序

1
2
3
4
5
6

from WindPy import *
w.start()

# 000001.SZ收益率为例
sy = w.wsd("000001.SZ", "pct_chg", "2018-07-05", "2018-07-11", "")
sy

.ErrorCode=0
.Codes=[000001.SZ]
.Fields=[PCT_CHG]
.Times=[20180705,20180706,20180709,20180710,20180711]
.Data=[[-0.11614401858303243,0.6976744186046501,4.272517321016162,-0.5537098560354228,-2.2271714922049117]]

1
2

sy2 = np.array(sy.Data[0])
sy2

array([-0.11614402,  0.69767442,  4.27251732, -0.55370986, -2.22717149])

1
2

# 对一个数组array，想找到其中大于0的数所在的索引位置 可以用where函数
print('大于0元素所在的索引：\n',np.where(sy2>0))

大于0元素所在的索引：
 (array([1, 2], dtype=int64),)

1
2

# 对于exp这个数组，希望对其按元素大小进行排序
print('从小到大排序：\n',np.sort(sy2))

从小到大排序：
 [-2.22717149 -0.55370986 -0.11614402  0.69767442  4.27251732]

1

print('排序后元素所在的原索引位置',np.argsort(sy2))

排序后元素所在的原索引位置 [4 3 0 1 2]

1.7 数组拼接

1

a1

array([8.6 , 8.66, 9.03, 8.98, 8.78])

1
2

a3 = np.array(w.wsd("000858.SZ", "close", "2018-07-05", "2018-07-11", "").Data)[0]
a3

array([70.82, 70.62, 73.54, 73.37, 72.08])

1
2
3

print('纵向拼接:\n',np.vstack((a1,a3)))
print()
print('横向拼接:\n',np.hstack((a1,a3)))

纵向拼接:
 [[ 8.6   8.66  9.03  8.98  8.78]
 [70.82 70.62 73.54 73.37 72.08]]

横向拼接:
 [ 8.6   8.66  9.03  8.98  8.78 70.82 70.62 73.54 73.37 72.08]

使用np.r_和np.c_也可以实现拼接的功能

注意纵向拼接的时候，np.c_产生的结果是5∗2，而np.r_产生的结果是2∗5

1
2
3

print('横向拼接：\n',np.r_[a1,a3])
print()
print('纵向拼接：\n',np.c_[a1,a3])

横向拼接：
 [ 8.6   8.66  9.03  8.98  8.78 70.82 70.62 73.54 73.37 72.08]

纵向拼接：
 [[ 8.6  70.82]
 [ 8.66 70.62]
 [ 9.03 73.54]
 [ 8.98 73.37]
 [ 8.78 72.08]]

1.8 数组分解

1
2

a4 = np.array(w.wsd("000858.SZ", "close,open,low", "2018-07-05", "2018-07-11", "").Data)
a4

array([[70.82, 70.62, 73.54, 73.37, 72.08],
       [71.69, 69.9 , 71.58, 73.57, 71.2 ],
       [69.7 , 68.88, 70.4 , 72.08, 70.93]])

1
2
3

print('横向分解为5个数组：\n',np.hsplit(a4,5))
print()
print('纵向分解为3个数组：\n',np.vsplit(a4,3))

横向分解为5个数组：
 [array([[70.82],
       [71.69],
       [69.7 ]]), array([[70.62],
       [69.9 ],
       [68.88]]), array([[73.54],
       [71.58],
       [70.4 ]]), array([[73.37],
       [73.57],
       [72.08]]), array([[72.08],
       [71.2 ],
       [70.93]])]

纵向分解为3个数组：
 [array([[70.82, 70.62, 73.54, 73.37, 72.08]]), array([[71.69, 69.9 , 71.58, 73.57, 71.2 ]]), array([[69.7 , 68.88, 70.4 , 72.08, 70.93]])]

二、常用数组

在工作或者学习中，有些数组是我们常用的，利用numpy中的函数可以容易地产生这些数组。

2.1 np.arange(起始数，终止数，间隔)

1
2
3
4

# np.arange()函数 终止数并不产生 
print(np.arange(1,10,1)) 
print()
print(np.arange(1,10,0.1))

[1 2 3 4 5 6 7 8 9]

[1.  1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.  2.1 2.2 2.3 2.4 2.5 2.6 2.7
 2.8 2.9 3.  3.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8 3.9 4.  4.1 4.2 4.3 4.4 4.5
 4.6 4.7 4.8 4.9 5.  5.1 5.2 5.3 5.4 5.5 5.6 5.7 5.8 5.9 6.  6.1 6.2 6.3
 6.4 6.5 6.6 6.7 6.8 6.9 7.  7.1 7.2 7.3 7.4 7.5 7.6 7.7 7.8 7.9 8.  8.1
 8.2 8.3 8.4 8.5 8.6 8.7 8.8 8.9 9.  9.1 9.2 9.3 9.4 9.5 9.6 9.7 9.8 9.9]

2.2 np.linspace(起始数,终止数,产生数的个数)

1
2
3
4
5

#在指定区间返回均匀间隔的数字
print(np.linspace(1,10,10))
print()
print(np.linspace(-1,1,20))
# np.linspace()函数 终止数是产生的

[ 1.  2.  3.  4.  5.  6.  7.  8.  9. 10.]

[-1.         -0.89473684 -0.78947368 -0.68421053 -0.57894737 -0.47368421
 -0.36842105 -0.26315789 -0.15789474 -0.05263158  0.05263158  0.15789474
  0.26315789  0.36842105  0.47368421  0.57894737  0.68421053  0.78947368
  0.89473684  1.        ]

2.3 常用矩阵

1
2
3
4
5

print('元素都为1的方阵：\n',np.ones((3,3)))
print()
print('元素都为0的方阵：\n',np.zeros((3,3)))
print()
print('单位阵：\n',np.eye(3))

元素都为1的方阵：
 [[1. 1. 1.]
 [1. 1. 1.]
 [1. 1. 1.]]

元素都为0的方阵：
 [[0. 0. 0.]
 [0. 0. 0.]
 [0. 0. 0.]]

单位阵：
 [[1. 0. 0.]
 [0. 1. 0.]
 [0. 0. 1.]]

2.4 np.tile()函数

该函数的作用是重复某个对象为一定的结构

1
2
3
4

short = np.arange(1,4,1)
print(short)
long = np.tile(short,3)
print(long)

[1 2 3]
[1 2 3 1 2 3 1 2 3]

1
2
3
4

small = np.eye(2)
print(small)
big = np.tile(small, (2,2))
print(big)

[[1. 0.]
 [0. 1.]]
[[1. 0. 1. 0.]
 [0. 1. 0. 1.]
 [1. 0. 1. 0.]
 [0. 1. 0. 1.]]

三、Numpy常用常量

1
2
3
4

print('自然底数：',np.e)
print('缺失值：',np.NaN)
print('无穷大：',np.inf)
print('圆周率：',np.pi)

自然底数： 2.718281828459045
缺失值： nan
无穷大： inf
圆周率： 3.141592653589793

四、Numpy随机数产生

1
2
3
4
5
6
7
8
9

print('一维正态随机数：\n',np.random.randn(5))
print()
print('二维正态随机数：\n',np.random.randn(2,2)) 
print()
print('二维0-1均匀分布随机数：\n',np.random.rand(2,2))   
print()
print('5个10-20的均匀随机整数：',np.random.randint(10,20,5))
print()
print('二维均匀随机整数：\n',np.random.randint(10,50,(2,2)))

一维正态随机数：
 [-0.65240628  1.07426523 -0.86730208 -0.91339241  1.20066541]

二维正态随机数：
 [[ 0.9663628  -1.32891237]
 [-0.54264665 -1.29035995]]

二维0-1均匀分布随机数：
 [[0.52527192 0.17719291]
 [0.10103986 0.41623399]]

5个10-20的均匀随机整数： [17 18 14 12 11]

二维均匀随机整数：
 [[38 24]
 [24 38]]

numpy.random函数

1
2
3
4
5

a = np.arange(1,11,1)
print(a)
np.random.shuffle(a)
print()
print('随机打乱a中的元素顺序：\n',a)

[ 1  2  3  4  5  6  7  8  9 10]

随机打乱a中的元素顺序：
 [10  3  2  6  1  9  8  7  4  5]

1
2
3

print(a)
print()
print('随机从a中选取5个元素：\n',np.random.choice(a,5))

[10  3  2  6  1  9  8  7  4  5]

随机从a中选取5个元素：
 [5 3 8 9 4]

五、Numpy矩阵性质

1
2
3
4
5
6
7
8
9
10
11
12

x = np.random.randint(1,10,(3,3))
print('原矩阵：\n',x)
print()
print('矩阵对角线：\n',np.diag(x))  
print()
print('矩阵上三角：\n',np.triu(x))  
print()
print('矩阵下三角：\n',np.tril(x))  
print()
print('矩阵的迹：\n',np.trace(x))  
print()
print('矩阵的转置：\n',x.T)

原矩阵：
 [[4 3 6]
 [2 7 1]
 [2 3 8]]

矩阵对角线：
 [4 7 8]

矩阵上三角：
 [[4 3 6]
 [0 7 1]
 [0 0 8]]

矩阵下三角：
 [[4 0 0]
 [2 7 0]
 [2 3 8]]

矩阵的迹：
 19

矩阵的转置：
 [[4 2 2]
 [3 7 3]
 [6 1 8]]

1
2
3
4

x = np.random.randint(1,10,(3,3))
print('原矩阵：\n',x)
print()
print('矩阵元素向右循环移动2位：\n',np.roll(x,2))

原矩阵：
 [[1 1 6]
 [7 3 3]
 [7 6 5]]

矩阵元素向右循环移动2位：
 [[6 5 1]
 [1 6 7]
 [3 3 7]]

六、Numpy矩阵运算

1
2

# numpy下的子模块linalg是一个线性代数运算库，关于矩阵运算主要使用该库来完成
import numpy.linalg as la

1
2
3

# 以000001行情数据为例
a5 = np.array(w.wsd("000001.SZ", "close,open,low", "2018-07-08", "2018-07-11", "").Data)
a5

array([[9.03, 8.98, 8.78],
       [8.69, 9.02, 8.76],
       [8.68, 8.89, 8.68]])

1
2
3
4
5
6
7
8
9

print('原矩阵：\n',a5)
print()
print('矩阵的行列式：\n',la.det(a5)) 
print()
print('矩阵的逆：\n',la.inv(a5)) 
print()
print('矩阵的特征值分解：\n',la.eig(a5))
print()
print('矩阵的奇异值分解：\n',la.svd(a5))

原矩阵：
 [[9.03 8.98 8.78]
 [8.69 9.02 8.76]
 [8.68 8.89 8.68]]

矩阵的行列式：
 0.0967539999999976

矩阵的逆：
 [[  4.31196643   1.11416582  -5.48607809]
 [  6.27984373  22.42801331 -28.98691527]
 [-10.74374186 -24.08479236  35.28949708]]

矩阵的特征值分解：
 (array([2.65036938e+01, 2.08824580e-01, 1.74815890e-02]), array([[-0.58362007, -0.78625042, -0.09211654],
       [-0.57657184,  0.5886538 , -0.64732544],
       [-0.57179763,  0.18787491,  0.75662693]]))

矩阵的奇异值分解：
 (array([[-0.58355077,  0.78217367, -0.21834112],
       [-0.5766266 , -0.58842029, -0.56680096],
       [-0.57181314, -0.20485584,  0.79439526]]), array([2.65057682e+01, 2.11310491e-01, 1.72745790e-02]), array([[-0.57510827, -0.58571691, -0.57112711],
       [ 0.81163598, -0.49595222, -0.30867203],
       [-0.10245733, -0.64106715,  0.76061515]]))

numpy.linalg函数

七、多项式曲线拟合

1
2

import matplotlib.pyplot as plt   # 导入作图库  为了更好展示曲线拟合的结果
plt.style.use('ggplot')

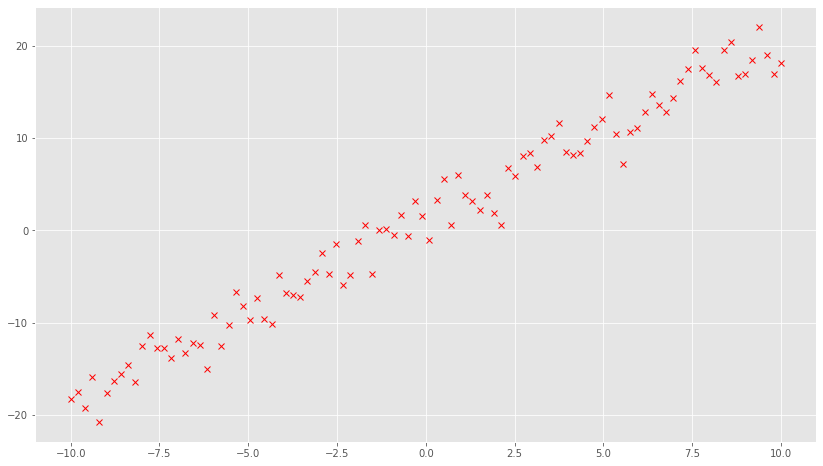
例如，对于下面的这些散点进行多项式拟合。观察散点的形态，采用直线取拟合

1
2
3
4
5

x = np.linspace(-10,10,100)
y = 2*x + 1 + np.random.randn(100)*2
fig = plt.subplots(figsize=(14,8))
plt.plot(x, y, 'rx')
plt.show()

1

from numpy import polyfit,poly1d

1
2

coef_fit = polyfit(x, y, 1)  #进行线性拟合 1代表的是多项式拟合的多项式的阶数  这里指的是线性拟合
coef_fit    #查看拟合的系数

array([1.96386726, 1.11375232])

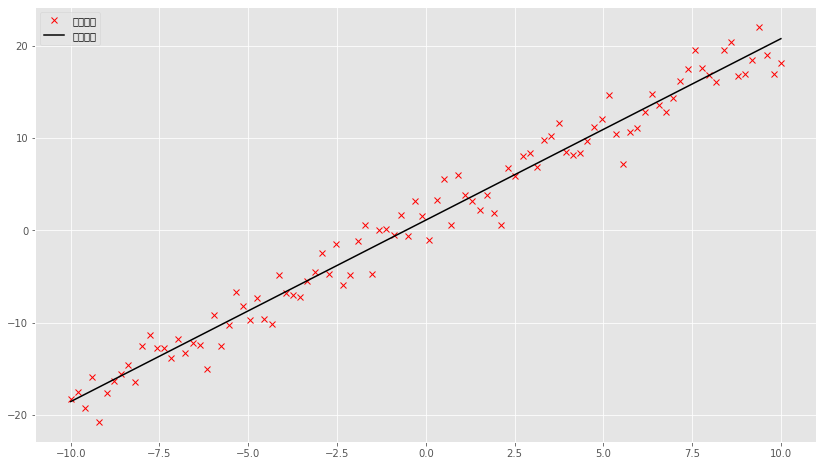
1
2
3
4
5

fig = plt.subplots(figsize=(14,8))
plt.plot(x, y, 'rx',label='真实散点')
plt.plot(x, coef_fit[0] * x + coef_fit[1], 'k-',label='拟合直线')
plt.legend(loc='best')
plt.show()

D:\anaconda\lib\site-packages\matplotlib\backends\backend_agg.py:211: RuntimeWarning: Glyph 30495 missing from current font.
  font.set_text(s, 0.0, flags=flags)
D:\anaconda\lib\site-packages\matplotlib\backends\backend_agg.py:211: RuntimeWarning: Glyph 23454 missing from current font.
  font.set_text(s, 0.0, flags=flags)
D:\anaconda\lib\site-packages\matplotlib\backends\backend_agg.py:211: RuntimeWarning: Glyph 25955 missing from current font.
  font.set_text(s, 0.0, flags=flags)
D:\anaconda\lib\site-packages\matplotlib\backends\backend_agg.py:211: RuntimeWarning: Glyph 28857 missing from current font.
  font.set_text(s, 0.0, flags=flags)
D:\anaconda\lib\site-packages\matplotlib\backends\backend_agg.py:211: RuntimeWarning: Glyph 25311 missing from current font.
  font.set_text(s, 0.0, flags=flags)
D:\anaconda\lib\site-packages\matplotlib\backends\backend_agg.py:211: RuntimeWarning: Glyph 21512 missing from current font.
  font.set_text(s, 0.0, flags=flags)
D:\anaconda\lib\site-packages\matplotlib\backends\backend_agg.py:211: RuntimeWarning: Glyph 30452 missing from current font.
  font.set_text(s, 0.0, flags=flags)
D:\anaconda\lib\site-packages\matplotlib\backends\backend_agg.py:211: RuntimeWarning: Glyph 32447 missing from current font.
  font.set_text(s, 0.0, flags=flags)
D:\anaconda\lib\site-packages\matplotlib\backends\backend_agg.py:180: RuntimeWarning: Glyph 30495 missing from current font.
  font.set_text(s, 0, flags=flags)
D:\anaconda\lib\site-packages\matplotlib\backends\backend_agg.py:180: RuntimeWarning: Glyph 23454 missing from current font.
  font.set_text(s, 0, flags=flags)
D:\anaconda\lib\site-packages\matplotlib\backends\backend_agg.py:180: RuntimeWarning: Glyph 25955 missing from current font.
  font.set_text(s, 0, flags=flags)
D:\anaconda\lib\site-packages\matplotlib\backends\backend_agg.py:180: RuntimeWarning: Glyph 28857 missing from current font.
  font.set_text(s, 0, flags=flags)
D:\anaconda\lib\site-packages\matplotlib\backends\backend_agg.py:180: RuntimeWarning: Glyph 25311 missing from current font.
  font.set_text(s, 0, flags=flags)
D:\anaconda\lib\site-packages\matplotlib\backends\backend_agg.py:180: RuntimeWarning: Glyph 21512 missing from current font.
  font.set_text(s, 0, flags=flags)
D:\anaconda\lib\site-packages\matplotlib\backends\backend_agg.py:180: RuntimeWarning: Glyph 30452 missing from current font.
  font.set_text(s, 0, flags=flags)
D:\anaconda\lib\site-packages\matplotlib\backends\backend_agg.py:180: RuntimeWarning: Glyph 32447 missing from current font.
  font.set_text(s, 0, flags=flags)

从上图可以看到，直线拟合的结果还是比较好的（报错可能是汉字bug

1
2

f = poly1d(coef_fit)   #也可以直接产生拟合的函数解析式
print('拟合函数：',f)

拟合函数：  
1.964 x + 1.114

氦核：numpy库很有“大计算器”的味道了，其实不会用的时候再去查也可以，主要是应该了解有什么基础功能，否则就会出现“自己实现某些基础算法”的乌龙（某种意义上也是好事，笑）。一起加油吧。

（完）

本文链接： https://konelane.github.io/2020/02/05/200205numpy/

-- EOF --