最后编辑于:2020.01.02 14:18
Valve-Steam“买断制”游戏平均价格时间序列模型
一、背景
作为精神文明消费品,游戏已成为每一个人或多或少都会接触的事物。游戏消费已经成为当代大学生重要的开支,而valve-steam游戏软件消费平台作为近乎垄断的最大的pc(个人电脑)游戏中介平台,已成为大多数电脑游戏玩家不可或缺的电脑软件。
很多游戏也有“年货”之称,而很多游戏的发布时机和销售价格都有一定的变化规律。本研究将基于steamspy中的steam游戏消费数据,希望探索对游戏的月平均价格的变化趋势。
(数据来源于steamspy)
二、变量说明
| 变量名 | 含义 | 变量水平 | 变量简介 |
|---|---|---|---|
| AVERAGE_PRICE | Steam平台上售卖的游戏的平均价格 | 连续型 | 发行游戏总价值/发行游戏总数 |
| Time | 月平均价格对应的时间 | 整数连续 | 04年1月到18年12月 |
Value-Steam平台售卖的游戏软件只计算了买断游戏的价格,不包括游戏内购项目的花费。因此本报告仅以“买断制”游戏的平均价格为研究对象。同时,为研究游戏市场整体的行情,我们不以游戏销量作为权重,单纯研究价格的变化趋势。
三、探索性数据分析
“买断制”游戏往往受公司销售业务安排的影响,拥有固定的折扣期,折扣期能很好地促进游戏的销量。value-steam游戏销售平台也拥有自己的折扣期,这使得游戏价格在原有基础上产生了上下波动的现象。
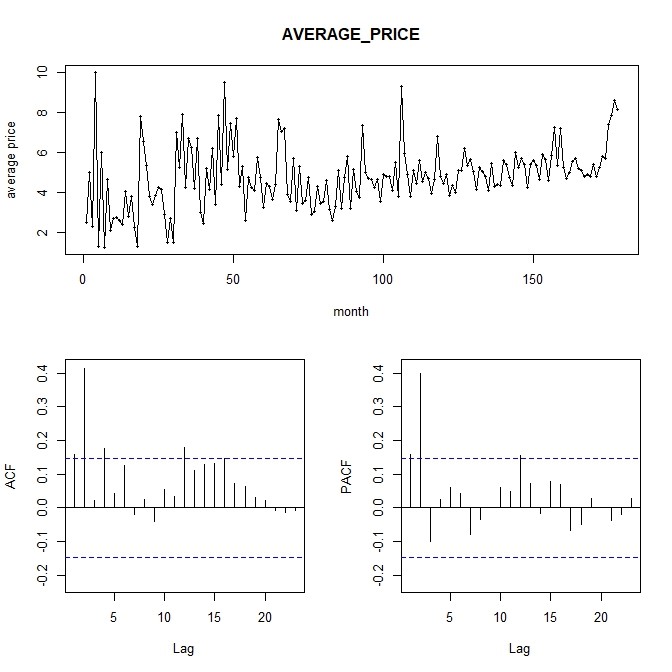
根据图1,我们能看出平均价格总体呈现增长趋势,并且有一定的波动模式。随机性趋势有但是不明显,且没有非常明显的季节趋势。
自相关图和偏相关图都表明有一定的自相关性,在二阶以前都存在显著不为零的部分,能够初步识别时间序列的ARIMA模型阶数。
四、模型探索
1.简单线性回归
首先使用简单线性回归模型对数据进行简单拟合。以AVERAGE_PRICE(平均价格)为因变量,以Time(时间)为自变量进行线性回归。
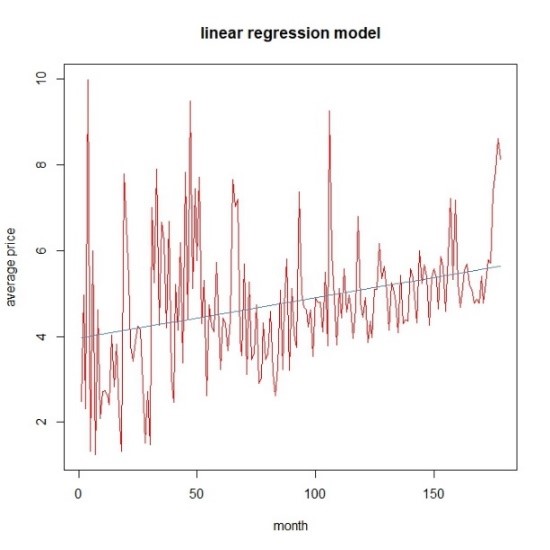
图二展示了用最小二乘线性模型拟合数据的结果,线性拟合只能拟合出线性增长的趋势,但是完全无法显示出随机波动的趋势。
| estimate | Std.error | T value | Pr(>t) | ||
|---|---|---|---|---|---|
| (Intercept) | 3.957189 | 0.222438 | 17.790 | < 2e-16 | *** |
| x | 0.009442 | 0.002155 | 4.381 | 2.03e-05 | *** |
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Multiple R-squared: 0.09832, Adjusted R-squared: 0.09319
F-statistic: 19.19 on 1 and 176 DF, p-value: 2.028e-05
虽然拟合参数都显著通过,通过观察调整的R方,我们能够看到模型的解释能力不足10%,拟合效果并不好。因此我们采取数据变换的方式尝试调整模型。
2.对数线性模型
对原始数据做对数变换,再使用线性模型拟合。
| estimate | Std.error | T value | Pr(>t) | ||
|---|---|---|---|---|---|
| (Intercept) | 1.2602098 | 0.0495757 | 25.420 | < 2e-16 | *** |
| x | 0.0028057 | 0.0004804 | 5.841 | 2.46e-08 | *** |
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Multiple R-squared: 0.1624, Adjusted R-squared: 0.1576
F-statistic: 34.11 on 1 and 176 DF, p-value: 2.459e-08
拟合参数依然显著通过,通过观察调整的R方,我们看出模型有了一定的优化,但依然拟合不好。可能不是数据的问题,所以接下来我们对模型进行调整。
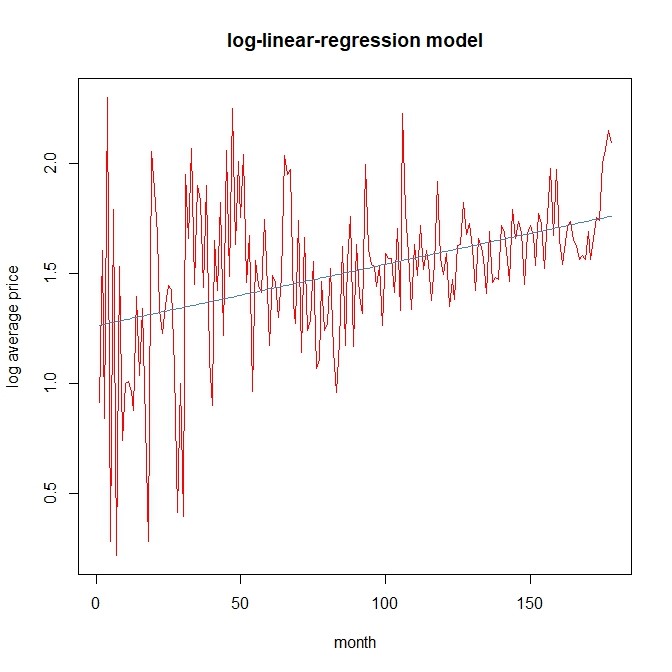
图3表明,对数变换后的数据虽然有很好的上升趋势,但是随机波动也随之变大,模型太过简单,损失了很多波动信息。不应采用。
五、时间序列模型识别
1.ARIMA时间序列模型
首先,我们对模型进行一阶差分,去数据的趋势,削减模型的不平稳性。
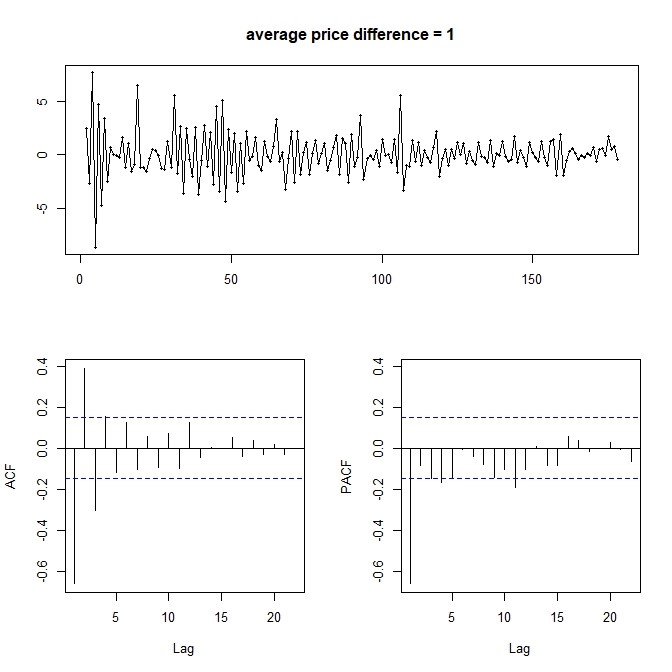
通过看到数据趋势基本消除,模型虽有波动,但是趋于规律。观察自相关函数和偏自相关函数,发现自相关性,初步推断模型是ma1与ar4的结合。通过R软件自动拟合,我们能够得到下表估计的模型系数。
| ar1 | ar2 | ar3 | ar4 | ma1 | intercept | |
|---|---|---|---|---|---|---|
| 系数 | 0.1020 | 0.3871 | -0.1103 | 0.0033 | -1.0000 | 0.0099 |
| s.e. | 0.0753 | 0.0757 | 0.0767 | 0.0811 | 0.0192 | 0.0032 |
sigma^2 estimated as 1.833: log likelihood = -307.08, aic = 628.15
我们发现ma1的系数为-1,该ARIMA模型不可逆,于是尝试增加一阶来拟合。利用R软件得到新拟合模型估计的参数。
|
ar1 |
ar2 |
ar3 |
ar4 |
ma1 |
ma2 |
intercept |
|---|---|---|---|---|---|---|---|
系数 |
-0.7327 |
0.4642 |
0.2125 |
-0.0646 |
-0.1614 |
-0.8385 |
0.0099 |
s.e. |
0.2219 |
0.0975 |
0.1262 |
0.0887 |
0.2085 |
0.2082 |
0.0032 |
sigma^2 estimated as 1.83: log likelihood = -306.91, aic = 629.81
可看到,如此调整,模型的aic有稍许的增加。但是模型平稳可逆,性质好。
2.模型评价
首先对模型残差进行shapiro正态性检验,利用R软件输出结果如下:
W = 0.93636, p-value = 4.695e-07
拒绝了残差正态性假定,说明模型拟合的还不够好。
接着分析模型自变量因变量的残差,进行Ljung-Box检验,利用R软件输出结果如下:
X-squared = 1.7957e-06, df = 1, p-value = 0.9989
对残差进行游程检验,p值0.881,不能拒绝其纯随机假定。
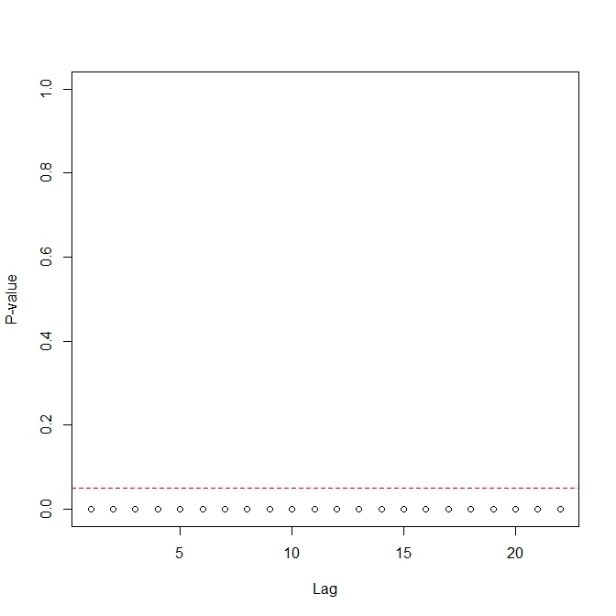
再进行McLeod-Li检验,看到模型不存在条件异方差。
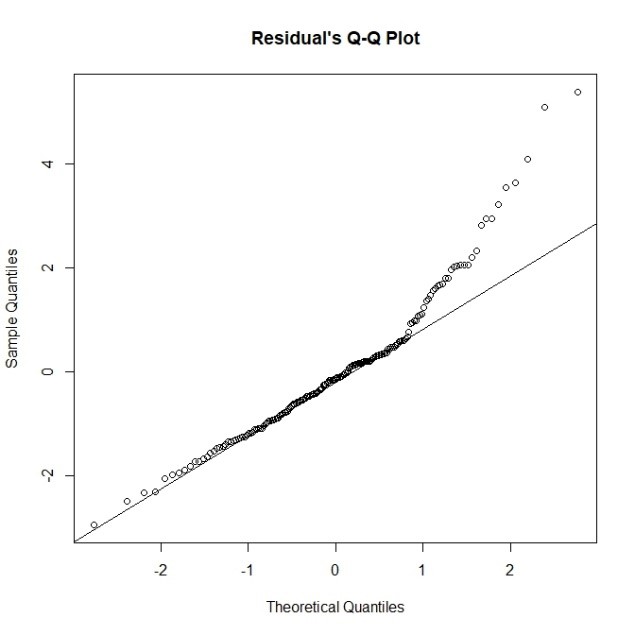
根据图5,观察模型残差的Q-Q图也可知残差无正态性。
以上分析表明,非季节项表明可以使用的模型为arima(4,1,2)或arima(4,1,1),考虑模型更好的性质,使用ARIMA(4,1,2)更优秀。
3.乘法季节模型
根据原始数据的PACF偏自相关(图7)看出,在季节性周期lags12处有spike,因此进一步做季节差分。
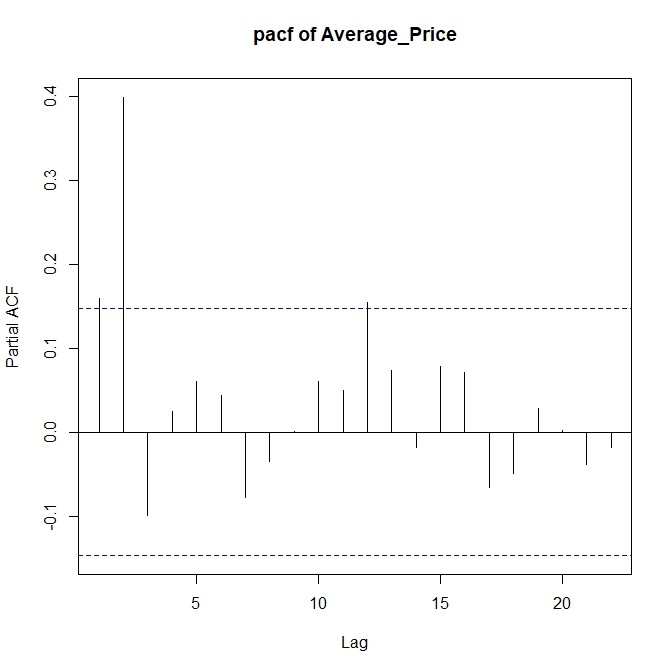
在进行季节差分后,对差分后数据进行探索性数据分析。画出趋势图、ACF和、PACF图进行研究。
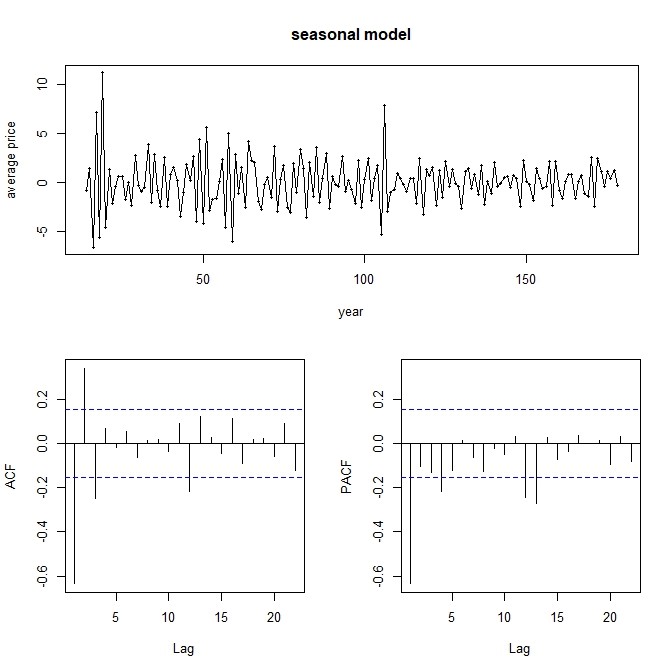
由图8能够看出,季节差分后,模型趋势几乎完全消失,只剩下周期性较强的波动和随机性特点。自相关函数和偏自相关函数都显示了模型的一定特征,再lag为12处依然能看出较强的相关性,但是其他位置也存在一定相关性。
所以对于非季节项,我们只做了一阶非季节差分,故d=1,从PACF看出p=4,从ACF看出q=2。
而对于季节项,也只做了一阶季节差分,故D=1,再看在lag12,24处看是否有spike,从PACF看出P=3,从ACF看出Q=1。
因此综上所述,识别阶段最终确定的模型为Arima(4,1,2)(1,1,3)[12]。
六、模型评估
利用R软件,对原始数据进行自动拟合分析,得到以下含有趋势的需要进一步差分。因为对aic计算时利用了近似,可能产生一定的误差。
| ARIMA(2,1,2) with drift | : 624.6381 |
|---|---|
| ARIMA(0,1,0) with drift | : 748.4041 |
| ARIMA(1,1,0) with drift | : 646.942 |
| ARIMA(0,1,1) with drift | : 647.6507 |
| ARIMA(0,1,0) | : 746.4034 |
| ARIMA(1,1,2) with drift | : 631.9857 |
| ARIMA(3,1,2) with drift | : 626.6319 |
| ARIMA(2,1,1) with drift | : 631.1114 |
| ARIMA(2,1,3) with drift | : 625.6269 |
| ARIMA(1,1,1) with drift | : 645.4117 |
| ARIMA(3,1,3) with drift | : 623.1056 |
| ARIMA(3,1,3) | : 621.1225 |
| ARIMA(2,1,3) | : 626.5835 |
| ARIMA(4,1,3) | : 608.4453 |
| ARIMA(4,1,2) | : 606.3408 |
| ARIMA(3,1,1) | : 624.4274 |
| ARIMA(5,1,3) | : 611.0288 |
| ARIMA(4,1,2) with drift | : Inf |
| ARIMA(3,1,2) | : 624.5451 |
| ARIMA(5,1,2) | : 609.452 |
| ARIMA(4,1,1) | : 612.635 |
Now re-fitting the best model(s) without approximations…
ARIMA(4,1,2) : 632.7907
|
ar1 |
ar2 |
ar3 |
ar4 |
ma1 |
ma2 |
|---|---|---|---|---|---|---|
系数 |
-0.3316 |
0.4072 |
0.0356 |
-0.0492 |
-0.5276 |
-0.3943 |
s.e. |
NaN |
NaN |
NaN |
0.0543 |
NaN |
NaN |
sigma^2 estimated as 1.971: log likelihood=-309.06
AIC=632.13 AICc=632.79 BIC=654.36
Best model: ARIMA(4,1,2),即依靠AIC筛选出非季节项的模型是ARIMA(4,1,2),模型的精确aicc为632.7907,bic为654.36,选取该模型和我们之前的分析的选择相同。
七、模型预测
用确定的模型Arima(4,1,2)(1,1,3)[12]预测接下来的五个阶段的平均价格。利用R软件得到的预测值见下表。
| Point Forecast | Lo 80 | Hi 80 | Lo 95 | Hi 95 | |
|---|---|---|---|---|---|
| 1 | 6.878770 | 5.079546 | 8.677993 | 4.127095 | 9.630444 |
| 2 | 6.508401 | 4.691427 | 8.325374 | 3.729579 | 9.287222 |
| 3 | 6.068549 | 4.087607 | 8.049491 | 3.038959 | 9.098139 |
| 4 | 6.042168 | 4.060691 | 8.023644 | 3.011761 | 9.072574 |
| 5 | 5.920171 | 3.904982 | 7.935360 | 2.838205 | 9.002137 |
Lo指下界,Hi指上界;80、95指显著性水平0.2、0.05。
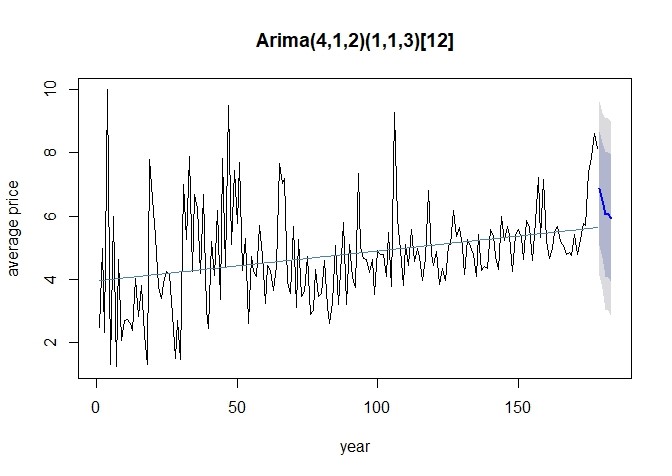
短期内呈现下降的波动趋势,但是长期来看却呈现上涨态势。预测区间较大,长期预测精确度不够。
八、原因探讨与结论
由于物价上涨,生活成本不断提高,游戏购买价格也随着游戏开发成本不断增加而上涨,但是由于游戏独特的促销手段,使其价格受折扣波动非常明显。而每年都有固定的折扣季,促进了游戏的消费。
但是同时需要注意的是,预测范围还是较大,长期精度较低,但是产业总体的发展趋势依然较好识别。建议消费者在购买游戏时,尽量赶在游戏的折扣期购买。相关企业进入市场时,也要注意游戏销售的价格。
参考文献
[1]刘杰华.2018年上半年游戏产业报告[R]. 北京: 伽马数据(CNG中新游戏研究).2018.
本文链接: https://konelane.github.io/2019/02/01/190201ts/
-- EOF --
转载请注明出处 署名-非商业性使用-禁止演绎 3.0 国际(CC BY-NC-ND 3.0)


